posted at 2021.6.26 15:36 by Administrator
这道难题流行于20世纪40年代,题目是给一名旅行商设计路线。让他以华盛顿特区为起点,周游美国本土的48个州。Julia Robinson建议把各州首府指定为旅行商的目的地,从而限制了路线的范围。求出最优路线。
那么,解决这道题目的算法有哪些呢?
一、最近邻算法
在从头开始构建路线的时候,最容易想到的方法就是每次都在没有到过的城市中选择最近的一个。这种算法称为最近邻算法(nearest-neighbor algorithm),看起来合情合理,然而得到的路线通常不是最短的。
二、贪心算法(greedy algoruthm)
贪心算法就是同时生成许多段子路线,每一步都把最短的可用路线片段加入解集中。
如果测试范例很大,若城市在正方形内随机分布,以直线距离作为每段路程,则贪心算法通常不会超过最优解的1.15倍,而最近邻算法通常不超过最优解的1.25倍。
三、插入算法(insertion algorithm)
这种算法的思路是从一条周游几个城市的子路线出发,逐个增加新的城市,让路线像橡皮筋一样扩展,从而包围更多城市。
插入算法可分为几种,分别为最小插入法(cheapest)、最近插入法(nearest)、最远插入法(farthest)、随机插入法(random)。无论是哪一种插入算法,在插入新城市时,都会选择路线上最合适的位点,使插入后的路线长度最短。
研究表明,在满足三角不等式的条件下,最小插入法和最近插入法都相当好,得到的路线长度不会超过最优路线长度的2倍。虽然在实际应用中,最远插入法往往效果最好,但在理论上,其路线长度只能保证不超过最优路线的log(n)倍。
四、深度优先搜索算法(depth-first search algorithm)
对于路线选择问题,最优解是一棵树,但树并不是环形路线,但是可以给出周游城市的方式。下面给出一种做法:在一棵树中,到达一座新城市后,如果有一条边从这座城市出发,尚未经过搜索,便沿这条边继续前进,到达另一座新城市;否则,如果从这座城市出发的所有边都已搜索过,则逐个回溯之前访问的城市,直到发现某座城市连接的某条边未经搜索为止。重复上述过程,最终会到达所有城市,并回到出发点。这样的路线称为按照深度优先搜索遍历一棵树。
五、Christofides算法
算法可以描述如下:
构造图上的最小的生成树T
令 O为原图顶点集中在T上度数为奇数的顶点集。根据握手定理,O中有偶数个顶点
构造点集O在原完全图上的最小完全匹配M
将 M 和 T 的边集取并,构造重图H ,满足其每个顶点都是偶数度的
H可以形成一个欧拉回路
将前一步得到的图改造为一个哈密尔顿回路:只需要跳过前一步欧拉回路中重复的顶点即可(这个步骤又称作选取近道,"short-cutting")。
1976年,Nicos Christofides首次完整提出这一算法,将欧拉和Edmonds的结论结合在一起,Christofides算法保证路线长度不超过最优解的1.5倍。
六、边交换算法
TSP领域,最基本的定理可能要数这一条:如果题目数据使用欧几里德距离,那么最优路线必定不会相交,用一步2-交换就可以证明这个事实。如果我们反复使用2-交换改进路线,就会大大改善差劲的最近邻路线。
七、Lin-Kernighan算法
20世纪60年代中期,Shen Lin发表了结果,证明3-交换可以成功地改进路线。但是,如果k远远大于2和3 ,搜寻改进路线的k-交换就需要巨大的计算量,因此完全不可行。尽管如此,Lin和计算机科学先驱Brian Kernighan还是成功实现了这种方法。他们巧妙地构建了一种新算法,取得了TSP研究中最伟大有成就之一。
Lin-Kernighan算法精巧复杂,但图一足以概述其中心思想。该图将初始路线表现为一个环,降低了理解算法流程的难度。需要提醒读者注意,各边在图中的长度并不代表实际路程。
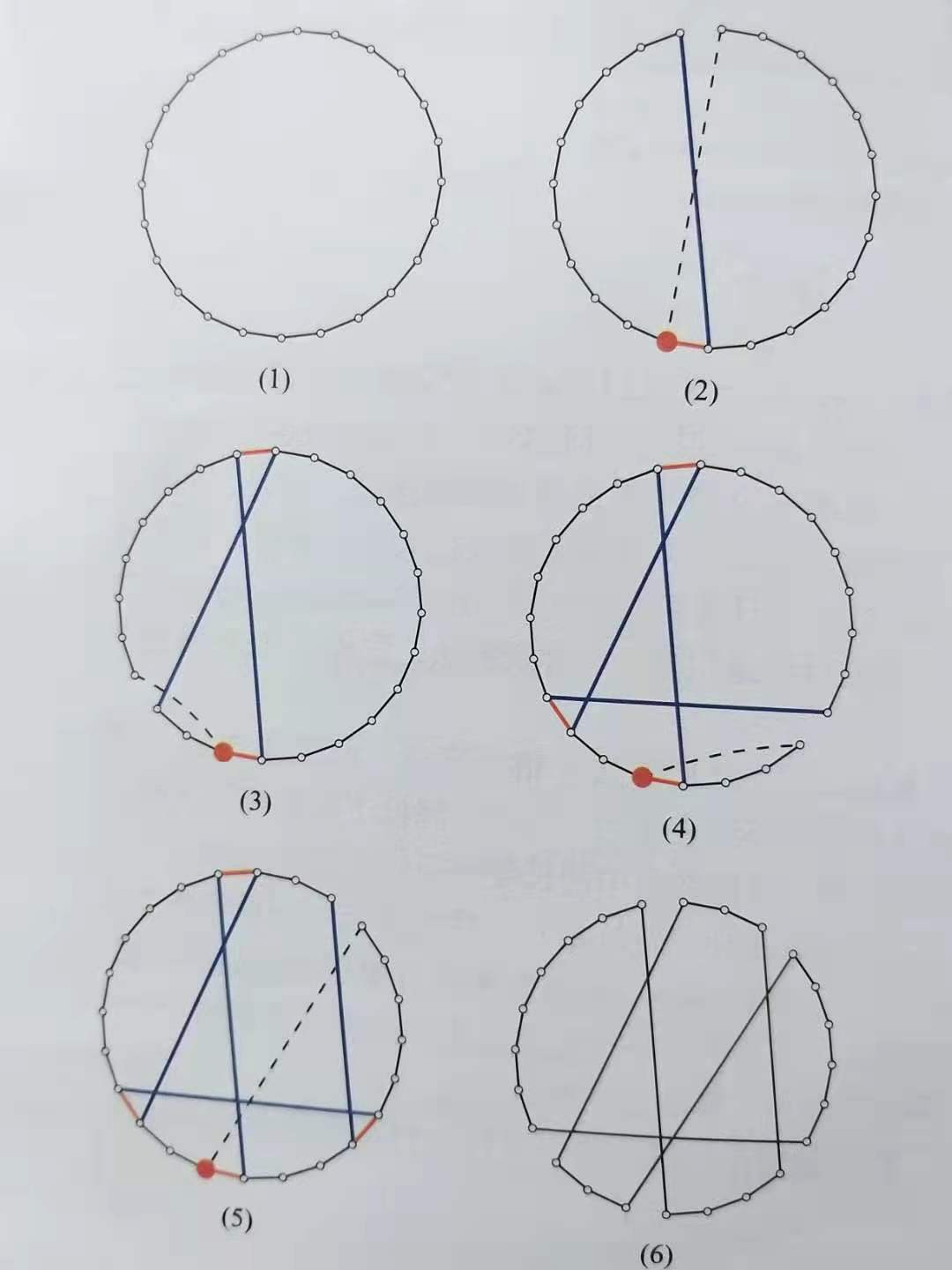
Lin-Kernighan算法使用随机路线作为初始路线,结果同样得到了环游美国问题的短路线。这为过去几十年中大多数优秀TSP解法奠定了基础,在此期间,规模大得多的题目也得以解决。
八、Lin-Kernighan-Helsgaun算法
Lin-Kernighan算法在实际计算领域长期占据统治地位。1998年。计算机科学家Keld Helsgaun带来了一枚重磅炸弹,他的主要贡献是重写了算法的核心搜索程序。Lin-Kernighan标准算法可以视为搜寻2-交换操作序列的方法,Helsgaun的新方法却以5-交换操作序列为搜寻对象,以愚公移山的努力,在性能方面实现了惊人的飞跃。
Helsgaun后来对LKH程序进行了有力的升级,允许用户具体指定每次交换操作包含连续几步。2003年,他以周游瑞典24978座城市的问题为例,计算了10-交换操作,所得TSP路线的最优性于次年得到证明。
九、借鉴物理和生物思想的算法
事实证明,把TSP视为一类搜索问题的特例,从全局着眼看待寻找路线过程,会大有裨益。思路意图产生元启发式算法(metaheuristic)。
(一)局部搜索与爬山算法
想象路线所处环境具有一定的地形变化,每条路线的高程对应于它的好坏程度,这样一来,启发式算法就可以想象成四处移动搜寻高地的过程。若搜寻全面彻底,则最终算法将在山峰上终止。
(二)模拟退火(simulated annealing)算法
该方法的动力源于统计力学与TSP的关联,在统计力学中,退火表示先加热再缓慢冷却材料以改善其结构的工艺过程。
(三)链式Lin-Kernighan算法
这种算法基本上垄断了20世纪90年代的路线搜寻领域。
(四)遗传算法(geneyic algorithm)
也有人从生物角度出发,把路线当成能够逐渐变异和进化的生命有机体。首先形成路线的初始“种群”,可以通过反复从随机城市出发使用最近邻算法获取路线。然后是一般的循环步骤,在种群中选取若干对路线,让它们“交配”(即交叉配对)得到子代路线,再从父子两代路线中选出一个新的种群。反复多次进行这一步骤,最优秀的路线最终将脱颖而出,成为唯一的生存赢家。
(五)蚁群优化算法(ant-colony optimization,ACO)
此类算法的工作原理是令一小群蚂蚁沿着图和各边移动,每只蚂蚁探寻一条路线,每次到达新顶点时都选择一条通向未访问的顶点的边。选择规则是算法的核心。
(六)其他
还有许多算法,如神经网络算法(neural network)、禁忌搜索算法(tabu search)和人工蜂群算法(honey bee)。
不知不觉,我们已经走了很远。毫无疑问,在研究TSP领域,丹麦人Keld Helsgaun和日本人永田裕一双双荣登世界冠军的宝座。对破记录的85900座城市TSP,Helsgaun的路线是绝对最优的。永田裕一也实现了一种TSP遗传算法,并以此求出了《蒙娜丽莎》TSP挑战的已知最佳路线,也给出了National TSP Collection中规模最大的两道题目的最佳答案。
我们并不宣称该程序万无一失,只是说它能在可行的计算时间内给出较好的结果。
—— Robert Karg 和 Gerald Thompson,1964年
10624be1-39bb-4158-b345-910442620b67|0|.0|96d5b379-7e1d-4dac-a6ba-1e50db561b04
Tags: 程序, 方法, 类, 模, 山, 数据, 算法, 物理
IT技术 | 生活艺术