posted at 2021.10.13 20:23 by 风信子

旅行商问题（TSP）是假设一个旅行商人要去n个城市，他必须经过且只经过每个城市一次，要求最后回到出发的城市，并且要求他选择的路径是所有路径中的最小值。

本文解决TSP问题使用的方法：模拟退火算法（Simulated Annealing Algorithm）。它是元启发式搜索算法的一种。相比起效率低下的随机搜索算法，元启发式搜索算法借助了演化思想和集群智能思想，对解的分布有规律的复杂问题有良好的效果。

模拟退火算法最早由N.Metropolis等人于1953年提出，基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。该算法从某一较高初温出发，伴随温度参数的不断下降，结合概率突跳特性在解空间随机寻找全局最优解。

模拟退火（Simulated Annealing）中的所谓退火是冶金专家为了达到某些特种晶体结构重复将金属加热或冷却的过程，该过程的控制参数为温度T。退火是将固体加热到足够高的温度，使分子呈随机排列态，然后逐步降温冷却，最后分子以低能状态排列，得到稳定状态的固体。

退火的过程有：

（1）加温过程：增强粒子运动，消除系统原本可能存在的非均匀态；

（2）等温过程：对于与环境换热而温度不变的封闭系统，系统状态的自发变化总是朝向自由能减少的方向进行，当自由能达到最小时，系统平衡；

（3）冷却过程：使粒子热运动减弱并逐渐趋于有序，系统能量逐渐下降，从而得到低能的晶体结构。

其中，固体在恒温下达到热平衡的过程采用Metropolis方法进行模拟：

温度恒定为T时，当前状态i转为新状态j，如果j状态的能量小于i，则接受状态j为当前状态；否则，如果概率p=exp{-(Ej-Ei)/(k*T)}大于[0,1)区间的随机数，则仍接受状态j为当前状态；若不成立则保留状态i为当前状态。

温度变化时，由于p=exp{-(Ej-Ei)/(k*T)}，因此在高温下，可接受当前状态能量差较大的新状态；在低温下，只接受与当前状态能量差较小的新状态。

退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

模拟退火法的基本思想是，在系统朝着能量减小的趋势这样一个变化过程中，偶尔允许系统跳到能量较高的状态，以避开局部极小点，最终稳定到全局最小点。

算法的关键问题是： 

初温与接受温度的设置

局部搜索的方法

退火系数 

某一温度下的内循环次数

  下面是模拟退火算法实现旅行商问题的C#代码：

    using System;

using System.Collections.Generic;

namespace ConsoleApp2

{

        class SimulatedAnnealingAlgorithm

        {

            const double STARTTEMPERATURE = 5000;             //初始温度

            const double ENDTEMPERATURE = 1e-8;               //结束温度

            const double Q = 0.98;                            //退火系数

            const int L = 1000;                               //每个温度最大迭代次数

            static int N = 34;                                //城市个数

     private static int[] CityResult = new int[N];          //城市列表的解空间,即下标

     private static int[] CityResultFirst = new int[N];                                               

     private static double[,] CityPoint = new double[34, 2];      //中国城市距离坐标

            public SimulatedAnnealingAlgorithm()

            {

                for (int i = 0; i < N; i++)

                {

                      CityResult[i]=i;

                      CityResultFirst[i] = i;

                }

                Console.WriteLine("最初顺序路径长度为：{0}\n", PathSum(CityResultFirst));

             }

            private static double PathSum(int[] list)

            {

                double distance = 0,sum=0,y0,y1;

                for (int i = 0; i < N - 1; i++)

                {

                    y0 = CityPoint[list[(i + 1) % (N-1)], 0];

                    y1 = CityPoint[list[(i + 1) % (N-1)], 1];

                    distance = Math.Sqrt((CityPoint[list[i], 0] - y0)

                                                    * (CityPoint[list[i], 0] - y0)

                                                    + (CityPoint[list[i], 1] - y1)

                                                    * (CityPoint[list[i], 1] - y1));

                    sum +=distance;

                }

                sum += Math.Sqrt((CityPoint[list[0], 0] - CityPoint[list[N - 1], 0])

                                            * (CityPoint[list[0], 0] - CityPoint[list[N - 1], 0])

                                            + (CityPoint[list[0], 1] - CityPoint[list[N - 1], 1])

                                            * (CityPoint[list[0], 1] - CityPoint[list[N - 1], 1]));

                return sum;         

             }

            private void CreateNewValue()                 //随机打乱

            {

                int p1, p2;

                Random r = new Random();

                p1 = r.Next(N);

                p2 = r.Next(N);

                var temp = CityResult[p1];

                CityResult[p1] = CityResult[p2];

                CityResult[p2] = temp;

             }

            private void SimulatedAnnealing()

            {

                int count = 0, i;//降温计数器

                int[] cityResult = new int[N];

                double path1, path2;    //原有解空间，新解空间的总路径

                double dE;              //原有解空间与新解空间的差值

                double r;               //随机产生0~1的值，是否接受新的解

                double t;               //当前温度

                t = STARTTEMPERATURE;   //初始温度赋值

                Random random = new Random();

                DateTime start = System.DateTime.Now;

                while (t > ENDTEMPERATURE)

                {

                    for (i = 0; i < L; i++)

                    {

                        cityResult = (int[])CityResult.Clone();

                        CreateNewValue();

                        path1 = PathSum(cityResult);

                        path2 = PathSum(CityResult);

                        dE = path2 - path1;

                        if (dE > 0)

                        {

                            //Metropolis准则：若Δt′< 0则接受S′作为新的当前解S，

                            // 否则以概率exp（-Δt′/ t）接受S′作为新的当前解S。

                            r = random.NextDouble();

                            if (Math.Exp(-dE / t) <= r)

                            //高温状态下，可以接受能量差值较大的新状态；低温状态下，则只能接受能量差值较小的新状态

                            {//保留原来的解

                                  CityResult = (int[])cityResult.Clone();

                            }

                        }

                    }

                    t *= Q;

                    count++;

                }

                DateTime end = System.DateTime.Now;

                Console.WriteLine("花费的时间为{0}", (end - start));

                Console.WriteLine("降温次数{0}", count);

                Console.WriteLine("经过模拟退火算法得出最优路径长度为：{0}\n",

                                                                       PathSum(CityResult));

                for (i = 0; i < N; i++)

                {

                   Console.Write("{0}->", CityResult[i]);                              

                }

                Console.Write("{0}\n", CityResult[0]); 

            }

            static void Main(string[] args)

            {

                CityPoint = new double[34, 2]{ {9932, 4439}, {10109, 4351}, {11552, 3472},

                        {10302, 3290}, {8776, 3333}, {7040, 4867}, {9252, 4278}, {9395, 4539},

                        {11101, 2540}, {9825, 5087}, {10047, 4879}, {10227, 4648}, {100027, 4229},

                         {9878, 4211}, {9087, 4065}, {10438, 4075}, {10382, 3865},

                        {11196, 3563}, {11075, 3543}, {11544, 3365}, {11915, 2900}, {11305, 3189},

                        {11073, 3137}, {10950, 3394}, {11576, 2575}, {12239, 2785}, {11529, 2226},

                        {9328, 4006}, {10012, 3811},  {9952, 3410}, {10612, 2954}, {10349, 2784},

                        {11747, 2469}, {11673, 2461} };    //实际坐标

                 new SimulatedAnnealingAlgorithm().SimulatedAnnealing();                        

             }

        }

     }

               代码显示图：

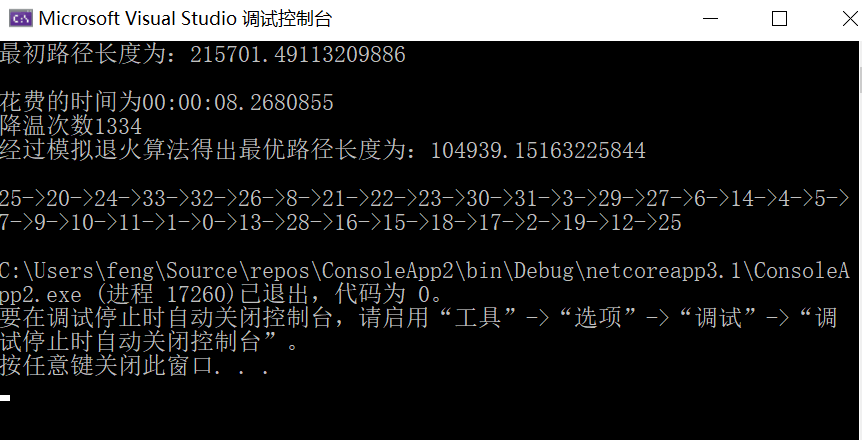
由测试结果可知，如果全局最优解不唯一，那么对于同一组输入数据，多次运行得到的路径也不相同。SA算法的效果依赖于链长、温度变化范围、控制参数等等，如果参数选取不合适将不能得到好的解。此外，实验过程中发现，在当前的参数（初始温度=5000，最大迭代系数=1000，alpha=0.98）情况下，问题能够得到圆满解决，也能够体现模拟退火算法在大规模问题下的高效性。

    我们可以得出结论： 

采用模拟退火算法具有超越算法本身的启发式意义。模拟退火算法将自然物理过程中的固体退火过程与组合优化问题进行类比，成功地将退火过程迁移用于旅行商问题，能够跳出局部最优状态范围。

 

鸣谢：本文C#代码(20211017）参考了

https://blog.csdn.net/weixin_44001521/article/details/105182126的代码