posted at 2022.7.1 11:04 by Administrator
Pell佩尔方程有着悠久迷人的历史,它首次被记载在“阿基米德牛群问题”中。该问题涉及8种花色的牛,各种线性关系已经给出,要求读者确定各种花色的牛的数量。经过一系列计算,这一问题最终简化成求解佩尔方程:
x2-4729494y2=1
最小解由Amthor最先于1880年确定,其中的y是一个41位数,看起来阿基米德及其同时代的人是不可能确定这个解的,但能想到这样一个问题是令人神魂颠倒的。
现代欧洲关于佩尔方程的历史始于1657年,当时费马向他的数学家朋友提出求解方程x2-61y2=1的挑战,其中几位数学家找到了最小解(x,y)=(1766319049,226153980)。1657年,布朗克尔(William Brouncker)描述了求解佩尔方程的一般方法,布朗克尔为了说明他的方法的有效性,仅用二个小时就求出方程:x2-313y2=1的一个解(32188120829134849,1819380158564160)。
沃利斯(J.Wallis)在一本关于代数与数论的书中描述了布朗克尔的方法,并且沃利斯和费马都断言佩尔方程总是有解的。欧拉错误地认为沃利斯书中的方法属于另一位英国数学家佩尔,并且正是欧拉将这个方程称为人们目前所熟知的“佩尔方程”。这个误解使佩尔获得了不朽的数学名声!
那么,如何求解佩尔方程
X2-Dy2=1
的一个正整数解x,y呢?因式分解
( x – y*D0.5)( x + y*D0.5) = 1 ,
将1表成两个数的乘积,其中一个相当大,更精确地说,x + y*D0.5相当大,尤其在x,y很大的时候更是如此,因此另一个因子
x - y*D0.5= 1 / ( x + y*D0.5)
必定相当小。
那么x-y*D0.5能小到何种程度?即|x-y*D0.5|<?。我们使用方法--鸽笼原理来求出结果。
首先认识“鸽笼原理”(抽屉原理或Schubfachschluβ)
这个奇妙的原理是说,如果鸽子比鸽笼多,那么至少有一只笼子里有两只以上的鸽子!尽管该原理看上去是明显和平凡的,但是恰当应用能产生丰富的数学成果。
我们将要做的是寻找两个不同的倍数x*D0.5和y*D0.5,使它们的差非常接近一个整数。为此,选择某个大数Y并考虑如下所有的倍数:
0*D0.5,1*D0.5,2*D0.5,3*D0.5,…,Y*D0.5。
将每一个倍数写成一个整数与一个介于0和他之间的小数之和。
0*D0.5=N0+F0 其中N0=0,F0=0。
1*D0.5=N1+F1 其中N1是整数,0≤F1 <1。
2*D0.5=N2+F2 其中N2是整数,0≤F2<1。
3*D0.5=N3+F3 其中N3是整数,0≤F13<1。
…
Y*D0.5=Ny+Fy 其中Ny是整数,0≤F1y<1。
我们这里的鸽子就是Y+1个数F0,F1,…,Fy。所有的鸽子都在0到1之间,所以它们全部落在区间0≤t<1中。我们将这个区间等分成Y个鸽笼,也就是说,将如下的区间取作鸽笼:
鸽笼1:0/Y≤t <1/Y。
鸽笼2:1/Y≤t <2/Y。
鸽笼3:2/Y≤t <3/Y。
…
鸽笼Y:(Y-1)/Y≤t <Y/Y。
每只鸽子都栖息在一个鸽笼中,且鸽子的数目多于鸽笼的数目,因此,鸽笼原理确保了某个鸽笼中至少有两只鸽子。比如,鸽子Fm和Fn栖息在同一个鸽笼中。将这两只鸽子做上标记使得m<n。注意到鸽笼相当狭窄,长度仅有1/Y,所以Fm与Fn之间的距离小于1/Y。用数学术语表示出来就是:
| Fm - Fn | < 1/Y。
下面利用
m*D0.5=Nm+Fm , n*D0.5=Nn+Fn
将上述不等式改写成
|(m*D0.5- Nm)-(n*D0.5- Nn)| < 1/Y。
即:
|(Nn - Nm)-(n-m)*D0.5 | < 1/Y。
注意到Nn - Nm和n-m都是(正)整数。如果分别将它们记作x,y,那么就完成了使|x-y*D0.5|相当小的目标。
通过试算x与 y*D0.5无限逼近1/y值,我们就可以求出(x,y)值。
C#程序代码:
private static string Pell(double D) { DateTime dt = DateTime.Now; double m = Math.Pow(D, 0.5); string result = "1"; double x=1,y=1,z; for (x = 1; x < 100000; x++) { for (y = 1; y < 100000; y++) { if (Math.Abs( x - m * y) < 1 / y) { z=Math.Pow(x,2)-Math.Pow(y,2)*D; result += "("+x.ToString()+","+y.ToString()+","+z.ToString()+")"; } else { } } } DateTime dt2 = DateTime.Now; TimeSpan timespan = dt2 - dt; Console.WriteLine("耗时{0}秒", timespan.TotalSeconds); return result; }
我们解决了佩尔方程的基本求解问题,但是,大家有没有注意到,运用上述C#程序求解佩尔方程解时,其运行时间为O(N2),非常缓慢。例如:求解x2-61y2=1,耗时54秒之多。
有没有快速求解程序呢?回答有。它是采用连分数数学特性求解佩尔方程。
首先我们理解连分数与佩尔方程定理:
记D0.5的连分数为
D0.5= [a,b1,b2,…,bm-1,bm]
并令p/q=[ a,b1,b2,…,bm-1],则佩尔方程
x2 - Dy2 = 1
的最小正整数解为
(x1,y1)等于
1、若m为偶数,为(p,q)
2、若m为奇数,(p2+q2D,2pq)。
其他所有的解均由公式
xk+yk*D0.5=(x1+y1*D0.5)k,k=1,2,3,…
给出。
下面举例说明求解x2-313y2=1:
3130.5=[17,1,2,4,11,1,1,3,2,2,3,1,1,11,4,2,1,34]
按定理所述,去掉周期部分的最后一个数字,即34,并计算分数
126862368/7170685 = [17,1,2,4,11,1,1,3,2,2,3,1,1,11,4,2,1]
周期m等于17,故(p,q)=(126862368,7170685)满足
1268623682-313·71706852=-1
为求出佩尔方程的最小解,根据定理,计算
P2+q2D=1268623682+313·71706852=32188120829134849
2pq=2·126862368·7170685=1819380158564160
于是x2-313y2=1的最小解为
(x,y)=( 32188120829134849, 1819380158564160)
如果要求下一个最小解,只需对
32188120829134849+1819380158564160·3130.5
平方即可得答案
(x,y)=(2072150245021969438104715652505601,
117124856755987405647781716823680)
C#程序代码:
private static string Lianfenshu(int D) //x^2-D*y^2=1中的D
{ int[] d = LianfenshuQuery(D); //int[] d= LianfenshuQueryDictionary(D); double[] zum=new double[d.Length+1]; zum[d.Length] = 0; zum[d.Length-1]=1; double sum =1; string result = ""; int x ; for (x = d.Length-2; x >=0; x--) { sum=d[x]*sum+zum[x+2]; zum[x] = sum; result += "(" + sum.ToString() + "," + x.ToString() + ")"; } if (d.Length%2!=0) { Console.WriteLine("最小解(" + zum[0].ToString() + ","+ zum[1].ToString() + ")") ; } else { double s= Math.Pow(zum[0], 2)+ Math.Pow(zum[1], 2)*D; double t = 2* zum[0]* zum[1]; Console.WriteLine("最小解("+s.ToString()+","+ t.ToString()+")"); } return result; } private static int[] LianfenshuQuery(int D) { int[][] lianfenshu=new int[360][]; lianfenshu[2]=new int[]{ 1, 2 }; lianfenshu[3] = new int[] { 1, 1, 2 }; lianfenshu[5] = new int[] { 2, 4 }; lianfenshu[6] = new int[] { 2, 2, 4 }; lianfenshu[7] = new int[] { 2, 1, 1, 1, 4 }; lianfenshu[8] = new int[] { 2, 1, 4 }; lianfenshu[10] = new int[] { 3, 6}; lianfenshu[11] = new int[] { 3, 3, 6 }; lianfenshu[12] = new int[] { 3, 2, 6 }; lianfenshu[13] = new int[] { 3, 1, 1, 1, 1, 6 }; lianfenshu[14] = new int[] { 3, 1, 2, 1, 6 }; lianfenshu[15] = new int[] { 3, 1, 6 }; lianfenshu[17] = new int[] { 4, 8 }; lianfenshu[18] = new int[] { 4, 4, 8 }; lianfenshu[19] = new int[] { 4, 2, 1, 3, 1, 2, 8 }; lianfenshu[20] = new int[] { 4, 2, 8 }; lianfenshu[55] = new int[] { 7, 2, 2, 2, 14 }; lianfenshu[61] = new int[] { 7, 1, 4, 3, 1, 2, 2, 1, 3, 4, 1, 14 }; lianfenshu[71] = new int[] { 8, 2, 2, 1, 7, 1, 2, 2, 16 }; lianfenshu[313] = new int[] { 17, 1, 2, 4, 11, 1, 1, 3, 2, 2, 3, 1, 1, 11, 4, 2, 1, 34 }; lianfenshu[4] = new int[] { 3,7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2 }; //Math.PI lianfenshu[9] = new int[] { 2,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,14 }; //e int[] result = lianfenshu[D]; return result; }
效果图:
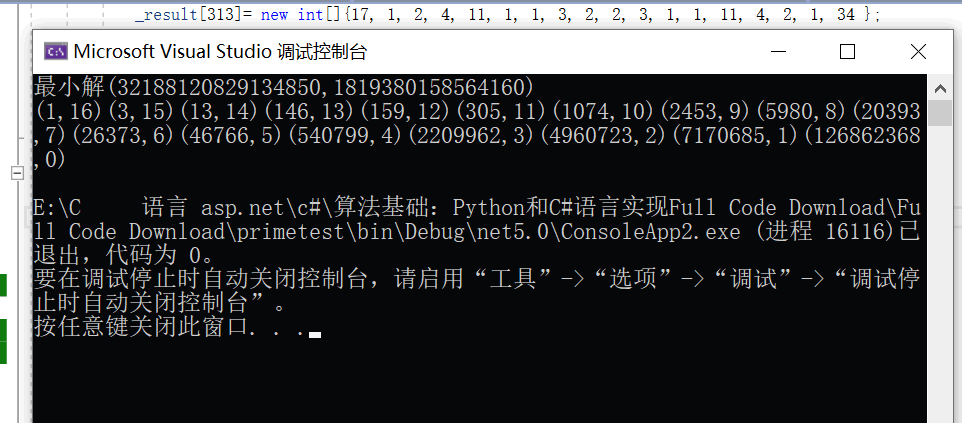
0a8013b0-039c-401f-aa6e-7e87ec500f36|0|.0|96d5b379-7e1d-4dac-a6ba-1e50db561b04
Tags: C#, 程序, 代码, 方法
IT技术