posted at 2020.2.19 05:47 by 风信子
德国哈勒的数学家格奥尔格•康托尔(Georg Cantor)在 100 多年前首先创立了集合论,如自然数的集合、所有分数的集合,还有有理数的集合。
所谓“势”,并不是指数字的范围或大小,而是其他东西。如果两个集合“等势”(一样大),打个比方,这两个集合里的元素可以办一场舞会,在这场舞会里,没有人会因为找不到舞伴而失落地看着别人跳舞。第一个集合里的一个元素和第二个集合里的一个元素组成了一对舞伴。
在等势的两个集合里, 两个集合中的每个元素都能找到一个舞伴, 没有人会被单独剩下。如果是 50 个女孩在舞会上遇到 30 个男孩,这就行不通了。因为女孩的集合的势比男孩的集合的势更大
当自然数和分数在一场舞会中相遇时,会发生什么呢?简单起见,我们这里只讨论正分数。每个分数都找到舞伴了吗?或者,有个别分数只能默默地旁观?
我们想当然地认为 :在两个自然数 0 和1之间存在无穷多个分数,如 1/2、1/3、1/4 ……因此,分数明显应该更多,尽管两个集合都包含有无穷多的元素。但是康托尔可以证明,自然数集和分数集等势——每个数字都保证能找到一个舞伴。
自然数是可数的——这很明显。从 0 开始数, 每个任意大的数字在某一刻都能被数到。由于有无穷多的自然数,我们可以说,自然数集是可数无穷的。这就是说 :我们可以把这个集合的所有元素都逐一编号。我从集合中取出的每一个元素,都具有一个编号。在自然数集合里,这个编号与自然数本身完全一一对应。但对于其他可数无穷集合,这不是那么容易实现的。
那么我们如何将无穷集合进行比较呢?很简单: 当一个集合同样是可数无穷时,这个集合就跟自然数集等势。它在分数集里表示就是:我随机选出一个元素,例如 2/3,然后就像在“他”的额头上贴上一个编3号。康托尔的功劳就是编出了一份指南,让我们能够计算这些编号。
康托尔证明正分数集和自然数集等势,是基于两种天才般的方法。首先,他设计了一张表格(见下表),在这个表格里,所有正分数都有它们固定的位置。你可以在这里看到这张表格的左上方部分——表格向右和向下无限延伸。
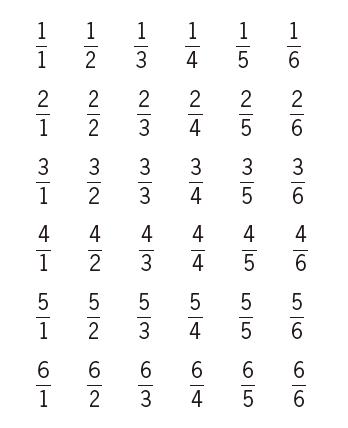
但是我们还不能够数完这张表里的所有数。例如,如果我们从第一行的左上角开始向右数,我们就将会无穷无尽地数下去,永远数不到第二行。
康托尔又准备好了第二招。他没有数一整行或一整列,而是从右上角到左下角斜着数,再从左下角向右上角数,以此类推。
用这种方式,从 1/1 开始的每个分数都会得到一个编号。例如 :1/2的编号为 2, 1/5的编号为15。如此,这位数学家就证明了正分数集与自然数集等势。

像康托尔这样通过对角线计数的技巧,来处理表格右侧和底部的无穷多的数字,是十分漂亮的方法。康托尔就像一名园丁,要修剪一片无穷大的草坪,于是他站在草坪的左上角,推着割草机呈“之”字形曲折前进。
摘自<你学的数学可能是假的:超简单有趣的数学思维>启蒙书
8ea3eb60-5a69-4bc2-aea8-02fd8b575ce9|0|.0|96d5b379-7e1d-4dac-a6ba-1e50db561b04
Tags: 方法
IT技术