posted at 2021.7.28 16:27 by Administrator
下面是最小费用最大流问题的一个实例，笔者使用Excel2010对此进行了剖析。
某公司有三个生产基地，分别为A1，A2，A3，现需要将三个基地生产的产品运送到C1，C2两个经销商手中，中间要经过B1，B2两个分销中心。如图所示（弧旁数字代表单位时间最大通过量和单位流量费用）。求把产品从生产基地运送到经销商手中的费用最小的最大运输量。
该问题是一个最小费用最大流问题。用线性规划方法求解此问题，分两步进行。
第一步：先求此网络的最大流。
该网络由于有3个发点（供应点）和2个收点（接收点）。所以增加一个虚拟的发点s，指向三个发点，其容量分别为发点A1、A2、A3的可供应量；同时增加一个虚拟的收点t，2个收点指向它，其容量分别为收点C1、C2的需求量。
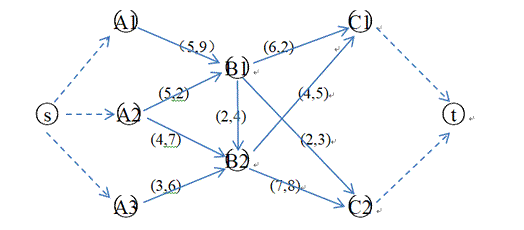
设fij表示从节点vi到vj的运输量（流量）；设F表示从s流出的流量或者是t流入的流量。该问题的数学模型可以表示为：
Max F=fsA1+fsA2+fsA3
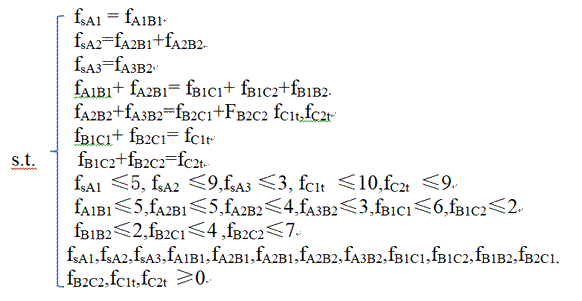
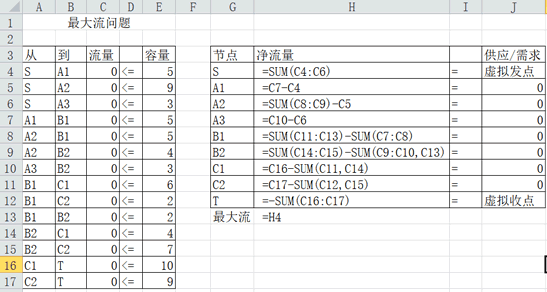
该问题的电子表格建模如图所示：
对该问题的电子表格进行求解如图所示：
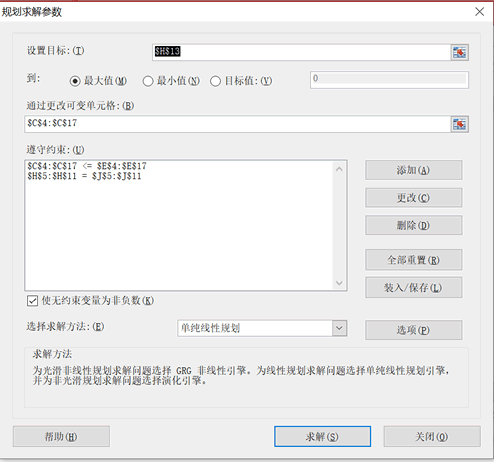
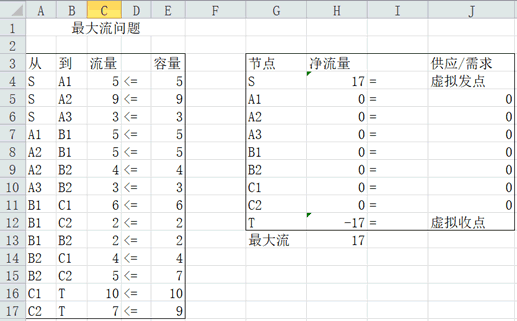
可以得出，从三个生产基地运送到两大经销商的最大运量为17。
第二步：求出在可获得的最大流（F=17）下，该网络的最小费用。
该问题的数学模型可以表示为：
Max F=9fA1B1+2fA2B1+7fA2B2+6fA3B2+2fB1C1+3fB1C2+4fB1B2+5fB2C1+8fB2C2
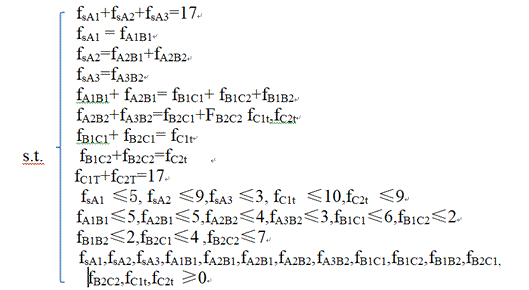该问题的电子表格建模如图所示：
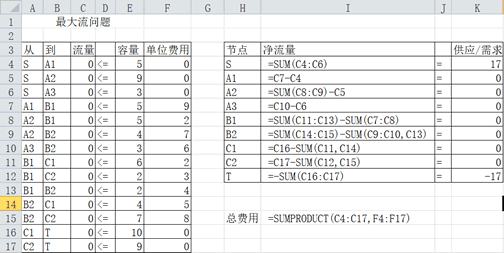
对该问题的电子表格进行求解如图所示：
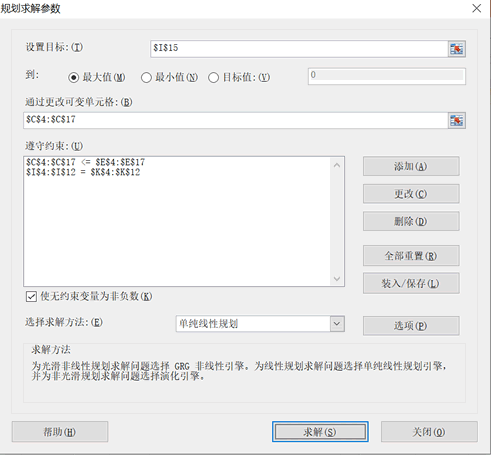
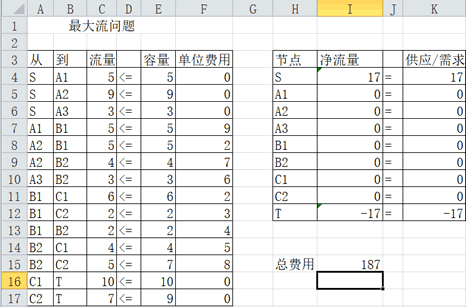
可以得出，从三个生产基地运送到两个经销商的最大运量为17时的最小费用为187。
bd273d9a-be2f-4e2b-8ce5-a49d91e182f5|0|.0|96d5b379-7e1d-4dac-a6ba-1e50db561b04
Tags: 方法, 模
IT技术 | 生活艺术
