posted at 2021.9.22 14:42 by 风信子
马踏棋盘是栈(STACK)的一个十分经典的应用。要求设计一个国际象棋的马踏遍棋盘的程序。将马随机放在国际象棋 8x8 棋盘的某个方格中,马按走棋规则进行移动。要求每个方格只进入一次,走遍棋盘上全部 64 个方格。
主要解决思想:
(一)使用图的深度优先搜索(DFS)回溯进行求解。这是一种十分暴力的处理方式,费时费力还不一定可以得到一个好的结果。
(二)使用贪心算法确定策略与优化方法进行求解,将每一步的下一步都进行贪心,便会节省大量的时间,而且成功率十分客观。
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题它能产生整体最优解或者是整体最优解的近似解。
下面具体使用贪心算法求解马踏棋盘问题:
一、编制递归或非递归程序
求出马的行走路线,并按求出的行走路线输出。
(1)将马行走路线以纵横坐标的形式输出。
(2)在方阵中输出 1~64 个马踏棋盘足迹。
二、数据定义
int X_Adrift 纵坐标
int Y_Adrift 横坐标
int Direction 方向
存储路径棋盘
int[,] Chess
下一步方向
一号
int[,] Dir = {{2,-1},{-2,-1},{-2,1},{2,1},
{1,-2},{-1,-2},{-1,2},{1,2}}
二号
int[,] Dir = {{1,2},{-1,-2},{-2,1},{2,1},
{2,-1},{1,-2},{-1,2},{-2,-1}}
三、基本思路
算法最核心的部分,是在下一步到底应该如何选择这件事上。
我们先判断下一步都有哪些位置可以走,然后我们再判断其可走位置的再下一步,有几个位置可以走,并统计这几个末端位置的在下一步有几个位置可以走。
即分别计算当前位置下下一步的权,之后我们将下下一步的权都加起来,算成下一步的权,并存储到 next 数组里面。之后,我们建立 realNext 数组,通过查找遍历,依次将 next 中最小元素的下标赋值给 realNext 数组,这样,我们就得到了一个下一步走的方向顺序的数组,按照 realNext 的顺序来走下一步。
四、方向顺序不同,路径存在不同。
下面,是不同方向同样初始(1,1)位置所得出的路径:
1号方向
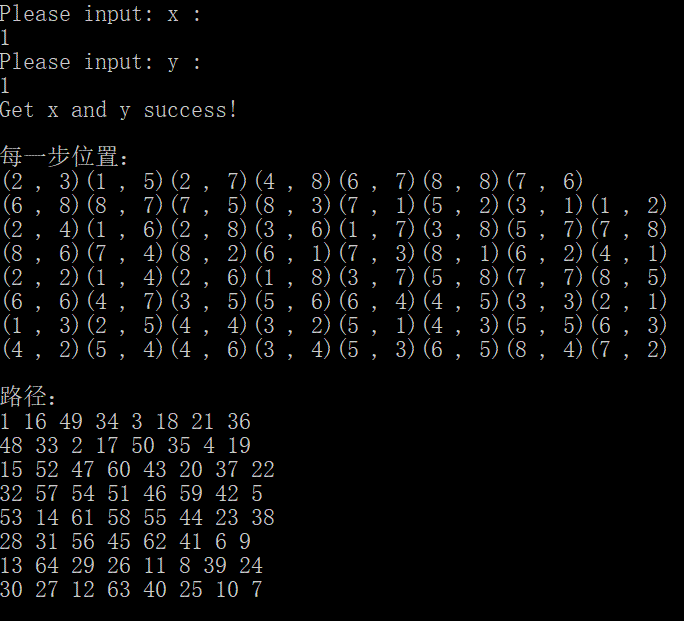
2号方向
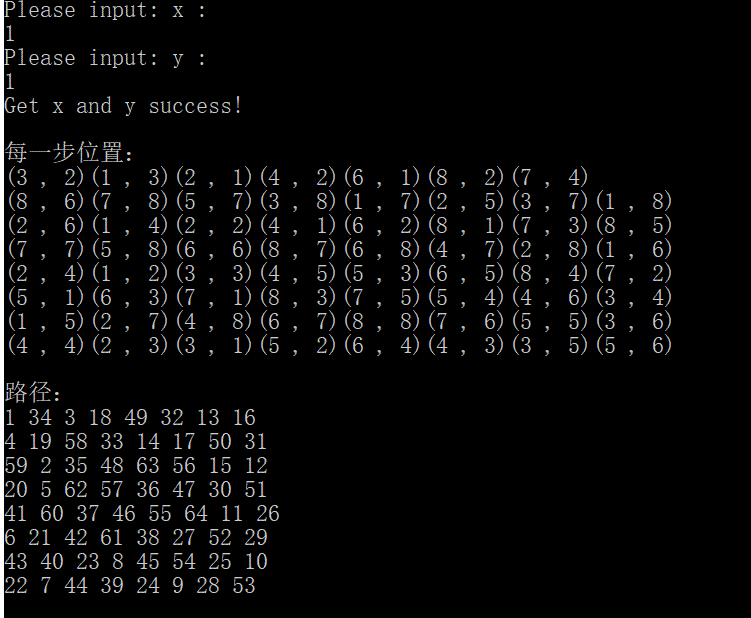
同时我们通过观察其用时发现,贪心算法的效率十分可观。
五、C#源代码
using System;using System.Collections.Generic;using System.Text;namespace ConsoleApp2{ class HorseGreedy { public class HorseMap { //栈结构体 struct HorseChessStack { public int X_Adrift; //纵坐标 public int Y_Adrift; //横坐标 public int Direction; //方向 } const int ROW = 8; const int COL = 8; const int MAX_STEPS = ROW * COL; //存储路径棋盘 public int[,] Chess=new int[ROW+1, COL+1]; //下一步方向 //一号 //public int[,] dir = {{2,-1},{-2,-1},{-2,1},{2,1}, // {1,-2},{-1,-2},{-1,2},{1,2}}; //二号 public int[,] Dir = {{1,2},{-1,-2},{-2,1},{2,1}, {2,-1},{1,-2},{-1,2},{-2,-1}}; //栈顶 public int Top; HorseChessStack[] AdriftStack=new HorseChessStack[MAX_STEPS]; //出栈次数 public int OutStack; //初始化数据 public void Init() { int n= MAX_STEPS; while(0<n) { n--; AdriftStack[n].X_Adrift = 0; AdriftStack[n].Y_Adrift=0; AdriftStack[n].Direction=-1; } AdriftStack[0].X_Adrift = 0; AdriftStack[0].Y_Adrift = 0; AdriftStack[0].Direction = -1; int i,j; for (i = 1; i <= ROW; i++) { for (j = 1; j <= COL; j++) { Chess[ROW, COL] = 0; } } Top = -1; OutStack = 0; } //入栈 public void PushStack(int xReal, int yReal) { Top++; AdriftStack[Top].X_Adrift = xReal; AdriftStack[Top].Y_Adrift = yReal; AdriftStack[Top].Direction = -1; //初始化走的方向 } //出栈 public void PopStack() { AdriftStack[Top].X_Adrift = 0; AdriftStack[Top].Y_Adrift = 0; AdriftStack[Top].Direction = -1; //初始化走的方向 Top--; } //标记位置 public void MarkChess(int x, int y) { Chess[y, x] = Top + 1; } //打印路径 public void PrintChessBoard() { Console.WriteLine(); Console.WriteLine("路径:"); int i, j; for (i = 1; i <= ROW; i++) { for (j = 1; j <= ROW; j++) { Console.Write("{0} ", Chess[i, j]); } Console.WriteLine(); } Console.WriteLine(); } //打印每一步的位置 public int t = 1; public void PrintSteps() { Console.Write("({0} , {1})", AdriftStack[Top].Y_Adrift, AdriftStack[Top].X_Adrift); t++; if (t == ROW) { Console.WriteLine(); t = 0; } } //马踏棋盘(贪心)算法 public void RunHorseTanxin() { int xNow, yNow; Console.WriteLine("每一步位置:"); while (1 == 1) { //已经走完全图 if (Top >= MAX_STEPS - 1) { //打印棋盘 PrintChessBoard(); break; } //现在位置 xNow = AdriftStack[Top].X_Adrift; yNow = AdriftStack[Top].Y_Adrift; //对方向进行排序 int[] next = new int[ROW]; int i, j; for (i = 0; i < ROW; i++) { //下一步坐标 int xNext = xNow + Dir[i, 0]; int yNext = yNow + Dir[i, 1]; if ((xNext > 0 && xNext <= COL) && (yNext > 0 && yNext <= ROW) && Chess[yNext, xNext] == 0) { //对下一步的下一步判断是否可以走 for (j = 0; j < ROW; j++) { int xNextNext = xNext + Dir[j, 0]; int yNextNext = yNext + Dir[j, 1];
//可以走,next 对应下标+1 if ((xNextNext > 0 && xNextNext <= COL) && (yNextNext > 0 && yNextNext <= ROW) && Chess[yNextNext, xNextNext] == 0) { next[i]++; } } } } //依次返回 next 中最小元素的下标,返回后将元素赋值为最大 int[] realNext = new int[8]; int k = 0; int t ; for (i = 0; i < ROW; i++) { t = ROW + 1; for (j = 0; j < 8; j++) { if (next[j] < t) { realNext[i] = j; t = next[j]; k = j; } } next[k] = ROW + 1; } //走下一步 int dirNow; for (dirNow = AdriftStack[Top].Direction + 1; dirNow < ROW; dirNow++) { int xReal = xNow + Dir[realNext[dirNow], 0]; int yReal = yNow + Dir[realNext[dirNow], 1]; AdriftStack[Top].Direction += 1; if ((xReal <= COL && xReal > 0) && (yReal <= ROW && yReal > 0) && Chess[yReal, xReal] == 0) { //入栈 PushStack(xReal, yReal); //标记棋盘 MarkChess(xReal, yReal); break; } } //如果下一步走不了,则出栈回溯 if (AdriftStack[Top].Direction >= 7) { Chess[AdriftStack[Top].Y_Adrift, AdriftStack[Top].X_Adrift] = 0; //记录出栈次数 OutStack++; PopStack(); } //打印栈 //打印 走了以后所处位置 PrintSteps(); } } } static void Main(string[] args) { HorseMap horseMap=new HorseMap(); int stX, stY; while (1==1) { Console.WriteLine("Please input: x :"); stX =Convert.ToInt32(Console.ReadLine()); Console.WriteLine("Please input: y :"); stY = Convert.ToInt32(Console.ReadLine()); if (stX > 0 && stX <= 8 && stY > 0 && stY <= 8) { Console.WriteLine("Get x and y success!\n"); break; }
Console.WriteLine("Input wrong!please input x y again:"); } horseMap.Init(); //将起始位置入栈 horseMap.PushStack(stX, stY); //标记起始位置 horseMap.MarkChess(stX, stY); //开始算法 horseMap.RunHorseTanxin(); } }}
鸣谢:C#源代码系根据
https://blog.csdn.net/weixin_43204126/article/details/102728758的C代码改写
e3b89308-2e0c-4f9c-9553-1489deebe526|0|.0|96d5b379-7e1d-4dac-a6ba-1e50db561b04
Tags: blog, C#, 程序, 代码, 方法, 数据, 算法
IT技术